有理数と無理数
数には、分数で表すことができる有理数と分数で表すことができない無理数があります。分数で表すことができるということは、2 つの数の比で表すことができるという意味ですのでそれぞれ有比数、無比数と読み替えてみると理解しやすいかもしれません。
有理数と無理数
有理数は分数で表すことができる数ですから、1/2 や 3/4 など、その例は簡単に示すことができます。また分数で表すことができるというのは必ずしも割り切れるという意味ではありません。たとえば 2/3 は 0.6666･･･ と６が繰り返し続く小数ですが分数で表すことができるので有理数です。また 2/7 は 0.285714285714･･･ と 285714が繰り返し続く小数ですがこれも有理数です。このように同じパターンを繰り返しながら無限に続く小数を循環無限小数といいます。
一方、無理数は分数で表すことができない数です。たとえば √2 や √3、円周率 π や自然対数の底 e などがあります。これらの数字は繰り返しのパターンがなく無限に続く小数です。
- √2 = 1.41421356237309504880･･･
- √3 = 1.73205080756887729352･･･
- π = 3.14159265358979323846･･･
- e = 2.71828182845904523536･･･
√2が開いた科学の扉
「万物は根源は数である」とし数の比がロゴスであると唱えたピタゴラス学派の哲学者たちにとって「数」とは有理数のことであり、有理数で表すことができない数は存在しないと考えていました。。
ところがピタゴラスの弟子のメタポンティオンのヒッパソスがこの考えを覆す発見をしました。ヒッパソスは正方形で三平方の定理（ピタゴラスの定理）を考えているうちに数と数の比で表すことができない無理数があることを発見したのです。
メタポンティオンのヒッパソス
三平方の定理は直角三角形の斜辺を c、残りの２辺を a、b とすると、c2 =a2 ＋b2 となる定理です。ヒッパソスは正方形の対角線の長さを三平方の定理で求めてみました。正方形の 2 辺 a、b と対角線 c でできる三角形は直角二等辺三角形になります。この場合、a と b を１とすると c2 =２となります。ヒッパソスは二乗すると 2 となる数字 c を数の比で表そうとしましたが絶対に無理であることに気が付いたのです。
三平方の定理（ピタゴラスの定理）
ヒッパソスはこの比で表すことができない数をピタゴラスに伝えました。ピタゴラスはヒッパソスの発見がピタゴラス教団の教えを覆すことになることを恐れてこのことを口外してはならないと命じました。おそらくヒッパソスは無理数の発見を隠すことはできなかったのでしょう。教団はこの発見を闇に葬るためにヒッパソスを処刑したと伝えられています。ピタゴラスは無理数の発見に驚愕し、その存在が世間に伝わることを警戒したに違いありません。
ヒッパソスが発見した無理数 c は √２です。ヒッパソスが無理数を発見したとき哲学者たちは混乱しました。しかし、やがて哲学者たちは混乱から脱却し有理数と無理数を合わせた実数という概念を作り上げました。実数の概念は数学を発展させることになり科学を発展させることにもなりました。
前ページ：2-08. 存在しないことを証明する背理法
前ページ 次ページ 目次次ページ：2-10. √2 は直線上に目盛りをつけられるか
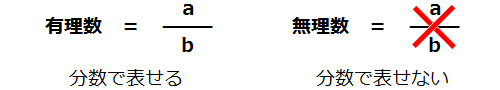
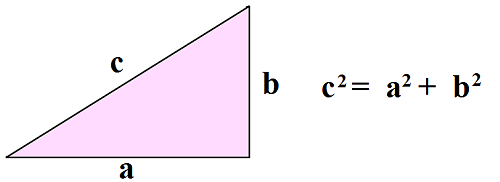
0 件のコメント:
コメントを投稿