超越数とは
代数的無理数で直線上の隙間がすべて埋まって稠密が実現できるかというと、実はそうではありません。無理数には代数で表すことができないものがあります。このような無理数を超越数といい円周率 π や自然対数の底 e などがあります。超越数は直線上に代数的無理数のような方法で目盛りをつけることができません。しかし直線上に π や e の目盛りをつけることは不可能ではありません。
直線上で円周率 π の位置を探す
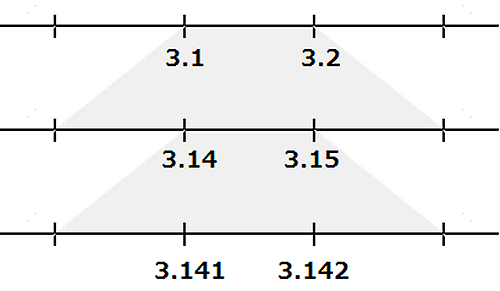
直線上で π の目盛りはどのようにつけることができるでしょうか。次の図のように 3.1 と 3.2 の間、3.14 と 3.15 の間、3.141 と 3.142 の間…というように、目盛りを細かく分割していくと、やがて π を示すであろう位置にたどり着くことができます。「π を示すであろう」と書いたのは π の値は無限に続く小数点だからです。
この方法では π が存在するであろう位置の範囲がどんどんせ狭められていきます。袋小路に追い詰めていくような方法ですが範囲を無限に狭めていけば、その範囲は限りなく0に近づいていくことになります。そこが π の目盛りを打つ位置となります。
このようにして、有理数、代数的無理数、超越数で直線を埋めると直線上に隙間がなくなります。このような状態を連続といいます。
ピタゴラス学派のアキレス腱
ピタゴラス学派は線分は最小単位の大きさをもつ点の集まりとしましたが、点は位置を示すもので大きさはありません。異なる位置を示す 2 つの点を結んだものが大きさをもつ線分です。しかしながら、点に大きさがないとすると 0を無限に足し算しても答えは0にしかなりませんから線分の存在に疑問符がつくことにならないでしょうか。だからこそ、ピタゴラス学派は線分は最小単位の大きさをもつ点の集まりとしたのでしょう。
ところで 1/n は n を大きくしていくと限りなく0に近づきます。これは直線を有理数で無限に分割できることを意味しています。有理数だけでつけた目盛りは数の比でつけられた目盛りであることには間違いありません。これはピタゴラス学派の思想に合致します。
この世界や宇宙が数の比によって秩序づけられているとしたピタゴラス学派にとって数の比で表すことができない無理数が発見されたことは非常に都合が悪いことだったのです。
前ページ:コラム 「定規」と「物差し」の違い
前ページ 次ページ 目次次ページ:2-12. ゼノンのパラドックス

0 件のコメント:
コメントを投稿